다익스트라 알고리즘이란?
다익스트라 알고리즘은 그래프에서 하나의 시작 정점으로부터 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이다. 가중치가 있는 그래프에서 최단 경로를 찾기 위해 사용되며, 음의 가중치를 가지는 간선이 없는 경우에 유효하다.
다익스트라 알고리즘은 주로 우선순위 큐를 사용하여 현재까지 발견된 최단 경로를 저장하고, 이를 기반으로 다른 정점으로의 경로를 지속적으로 업데이트하는 방식으로 작동한다.
다익스트라 알고리즘 구현
문제 설명
아래와 같은 가중치 그래프가 있다고 할 때, 1번 정점에서 모든 정점으로 가는 최소 거리 비용을 출력하라. (없으면 Impression 출력)

코드 구현
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
public class 다익스트라알고리즘 {
static class Edge implements Comparable<Edge>{
public int vex;
public int cost;
Edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
@Override
public int compareTo(Edge ob){
return this.cost - ob.cost;
}
}
static int n, m;
static ArrayList<ArrayList<Edge>> graph;
static int[] dis;
public void solution(int v){
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(v, 0));
dis[v] = 0;
while(!pQ.isEmpty()){
Edge tmp = pQ.poll();
int now = tmp.vex;
int nowCost = tmp.cost;
if(nowCost > dis[now]) continue;
for(Edge ob : graph.get(now)){
if(dis[ob.vex] > nowCost + ob.cost){
dis[ob.vex] = nowCost + ob.cost;
pQ.offer(new Edge(ob.vex, nowCost + ob.cost));
}
}
}
}
public static void main(String[] args){
다익스트라알고리즘 T = new 다익스트라알고리즘();
n = 6; // 노드의 개수
m = 9; // 간선의 개수
graph = new ArrayList<ArrayList<Edge>>();
for(int i = 0; i <= n; i++){
graph.add(new ArrayList<Edge>());
}
dis = new int[n + 1];
Arrays.fill(dis, Integer.MAX_VALUE);
// 간선 정보 직접 입력
int[][] edges = {
{1, 2, 12},
{1, 3, 4},
{2, 1, 2},
{2, 3, 5},
{3, 4, 5},
{4, 2, 2},
{4, 5, 5},
{4, 6, 5},
{6, 4, 5}
};
for(int[] edge : edges){
int a = edge[0];
int b = edge[1];
int c = edge[2];
graph.get(a).add(new Edge(b, c));
}
T.solution(1);
for(int i = 2; i <= n; i++){
if(dis[i] != Integer.MAX_VALUE) System.out.println(i + " : " + dis[i]);
else System.out.println(i + " : impossible");
}
}
}
그래프 초기화
노드와 간선 정보를 입력받아 그래프를 초기화한다.
n = 6;
m = 9;
graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}

거리 배열 초기화
dis = new int[n + 1];
Arrays.fill(dis, Integer.MAX_VALUE);
간선 정보 입력
int[][] edges = {
{1, 2, 12},
{1, 3, 4},
{2, 1, 2},
{2, 3, 5},
{3, 4, 5},
{4, 2, 2},
{4, 5, 5},
{4, 6, 5},
{6, 4, 5}
};
for (int[] edge : edges) {
int a = edge[0];
int b = edge[1];
int c = edge[2];
graph.get(a).add(new Edge(b, c));
}
다익스트라 알고리즘 실행
public void solution(int v){
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(v, 0));
dis[v] = 0;
while(!pQ.isEmpty()){
Edge tmp = pQ.poll();
int now = tmp.vex;
int nowCost = tmp.cost;
if(nowCost > dis[now]) continue;
for(Edge ob : graph.get(now)){
if(dis[ob.vex] > nowCost + ob.cost){
dis[ob.vex] = nowCost + ob.cost;
pQ.offer(new Edge(ob.vex, nowCost + ob.cost));
}
}
}
}
초기 상태
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(1, 0));
dis[1] = 0;
첫 번째 반복
추출된 노드: (1, 0)
인접 노드 업데이트: (2, 12), (3, 4)
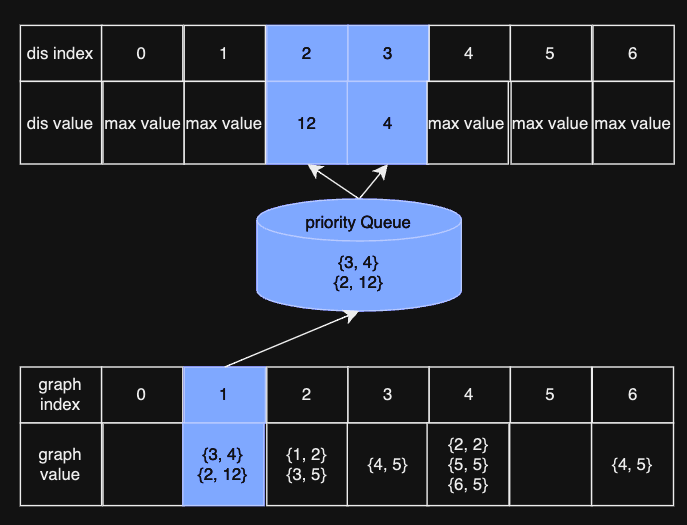
두 번째 반복
추출된 노드: (3, 4)
인접 노드 업데이트: (4, 9)

세 번째 반복
추출된 노드: (4, 9)
인접 노드 업데이트: (2, 11), (5, 14), (6, 14)

네 번째 반복
추출된 노드: (2, 11)
인접 노드 업데이트: (1, 13), (3, 16) - 이미 더 짧은 경로가 존재함

다섯 번째 반복
추출된 노드: (5, 14)
인접 노드 업데이트: 인접 노드 업데이트 없음.

여섯 번째 반복
추출된 노드: (6, 14)
인접 노트 업데이트: 인접 노드 업데이트 없음.

일곱 번째 반복
추출된 노드: (2, 12)
인접 노드 업데이트: 인접 노드 업데이트 없음.

결과 출력
for (int i = 2; i <= n; i++) {
if (dis[i] != Integer.MAX_VALUE) System.out.println(i + " : " + dis[i]);
else System.out.println(i + " : impossible");
}2 : 11
3 : 4
4 : 9
5 : 14
6 : 14'컴퓨터 공학 > 알고리즘' 카테고리의 다른 글
| Dynamic Programming의 개념과 종류, 사용 가능 조건과 예제(feat:Optimization Problem) (1) | 2024.12.15 |
|---|---|
| (알고리즘) Disjoint Set (Union-Find) (0) | 2024.06.22 |
