최적화(Optimization)
먼저 최적화에 대해 알아보기 전에 모델링의 매커니즘에 대해서 알아보자
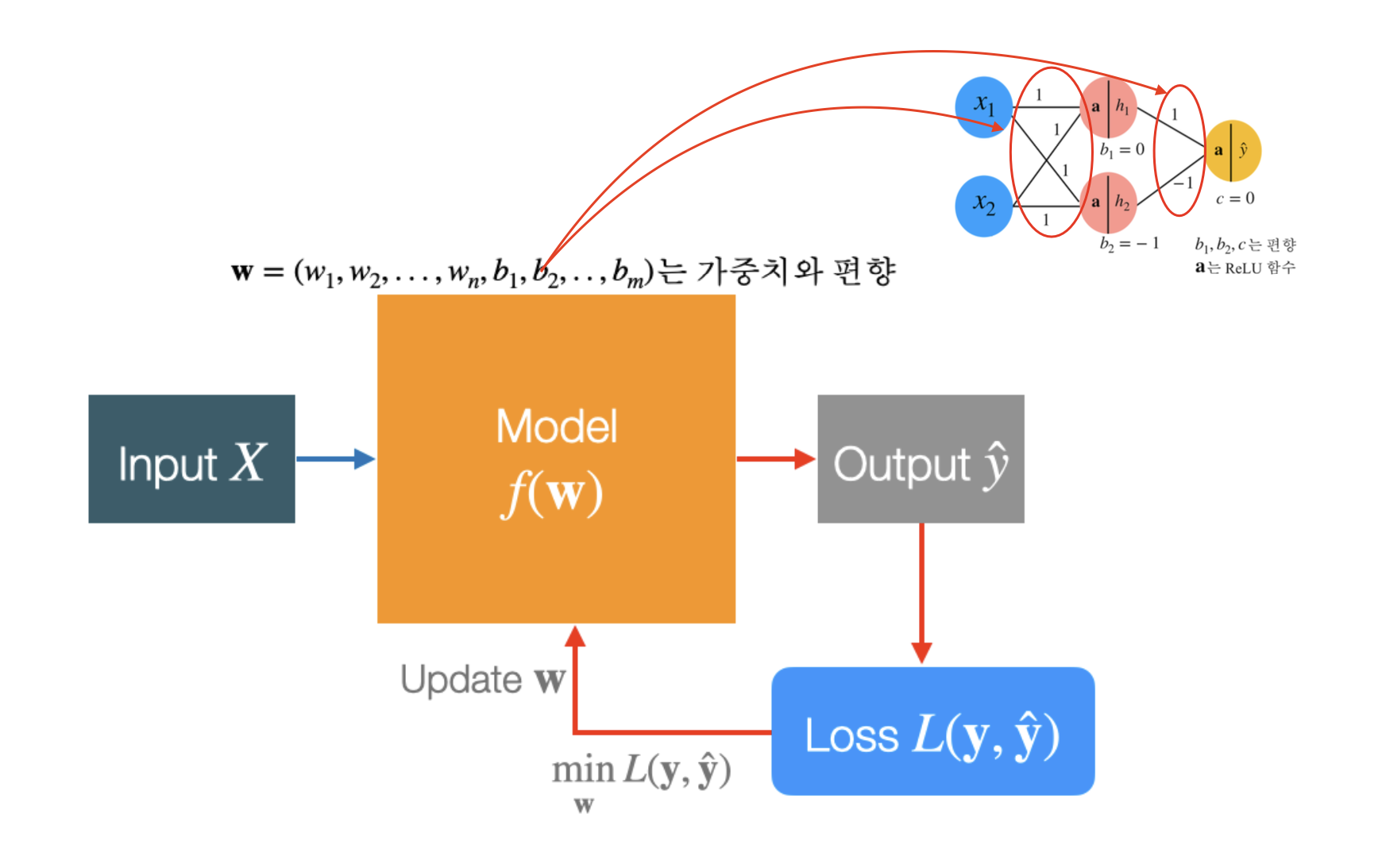
기본적으로 입력 값 X가 주어졌을 때, 모델을 통해 예측 값을 도출하고, 그 예측 값을 손실 함수에 넣어서 손실을 계산하게 된다. 손실 함수의 역할은 모델이 얼마나 잘 예측했는지를 평가하는 것이며, 손실 값이 작을수록 더 좋은 모델이라는 의미이다.
따라서 우리의 궁극적인 목표는 손실 함수의 값을 최소화하는 w(모델의 파라미터)를 찾는 것이다. 이 w는 모델이 데이터를 잘 설명할 수 있도록 최적화된 값이다.
모든 학습 과정의 핵심은 최적의 w를 찾는 것이며, 이를 위해 다양한 최적화 알고리즘 (예: 경사하강법, Adam 등)이 사용된다. 이러한 알고리즘들은 반복적으로 w를 업데이트하며 손실 함수를 최소화하도록 조정해준다. 최적의 w를 찾으면, 그 값을 최종적으로 모델에 적용하여 새로운 데이터에 대한 예측을 수행하게 된다.
즉 최적화란 최적화된 모델의 파라미터를 구하는 과정이라고 보면 될 것 같다.
목적 함수(Objective Function)
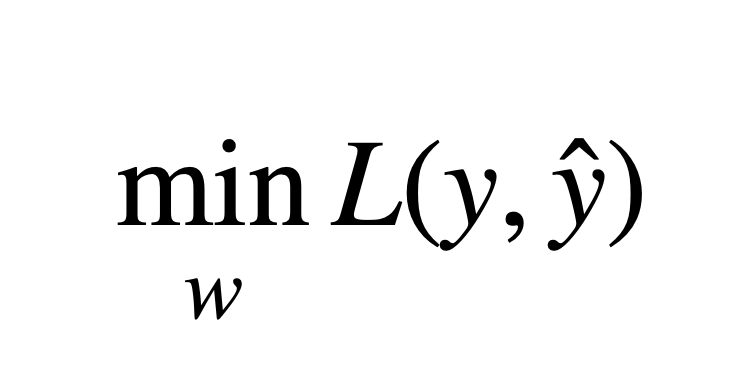
목적 함수는 모델이 학습하는 과정에서 최적화하려는 함수를 말한다. 손실 함수나 비용 함수와 같은 용어로도 자주 불리지만, 본질적으로 우리가 최대화하거나 최소화하려는 함수를 뜻한다.
예를 들어, 회귀 문제에서는 보통 손실 함수를 최소화하는 것이 목적이 되고, 분류 문제에서는 정확도나 우도 함수를 최대화하는 것이 목적이 된다. 정리하자면, 목적 함수는 모델이 학습하는 동안 최적화하는 대상 함수이며, 이를 통해 모델이 점점 더 좋은 성능을 내도록 만드는 과정에서 중요한 역할을 한다.
하강법
하강법은 손실 함수를 최소화하기 위해 사용되는 최적화 방법 중 하나다.
기본 개념은 매우 간단한데, 현재 위치에서 손실 함수의 기울기를 계산하고, 그 기울기를 따라 조금씩 아래로 내려가면서 최솟값을 찾는 과정을 뜻한다. 기본적으로 경사하강법(Gradient Descent)이라고 불리며, 매번 기울기(gradient)를 계산해 파라미터를 조금씩 업데이트하는 방식으로 작동한다. 기울기가 가리키는 방향이 손실이 가장 급격히 줄어드는 방향이기 때문에, 이 방향을 따라가면서 파라미터를 조정해 최적의 값에 수렴하게 된다.
하강법의 종류
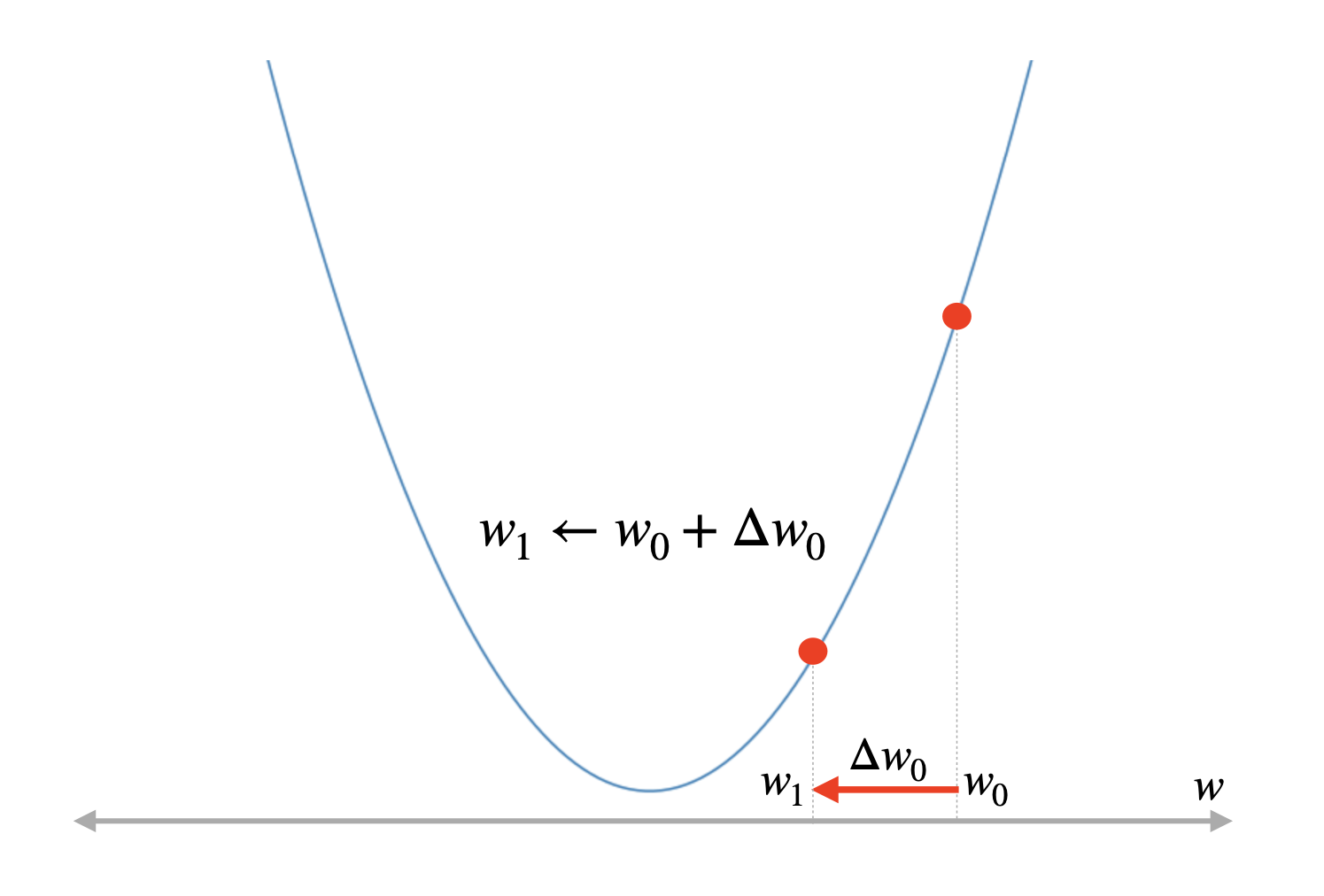
이떄 의문이 생긴다.
- 어디로 움직여야 최적의 방향을 찾기 위해 하강할 수 있는가?
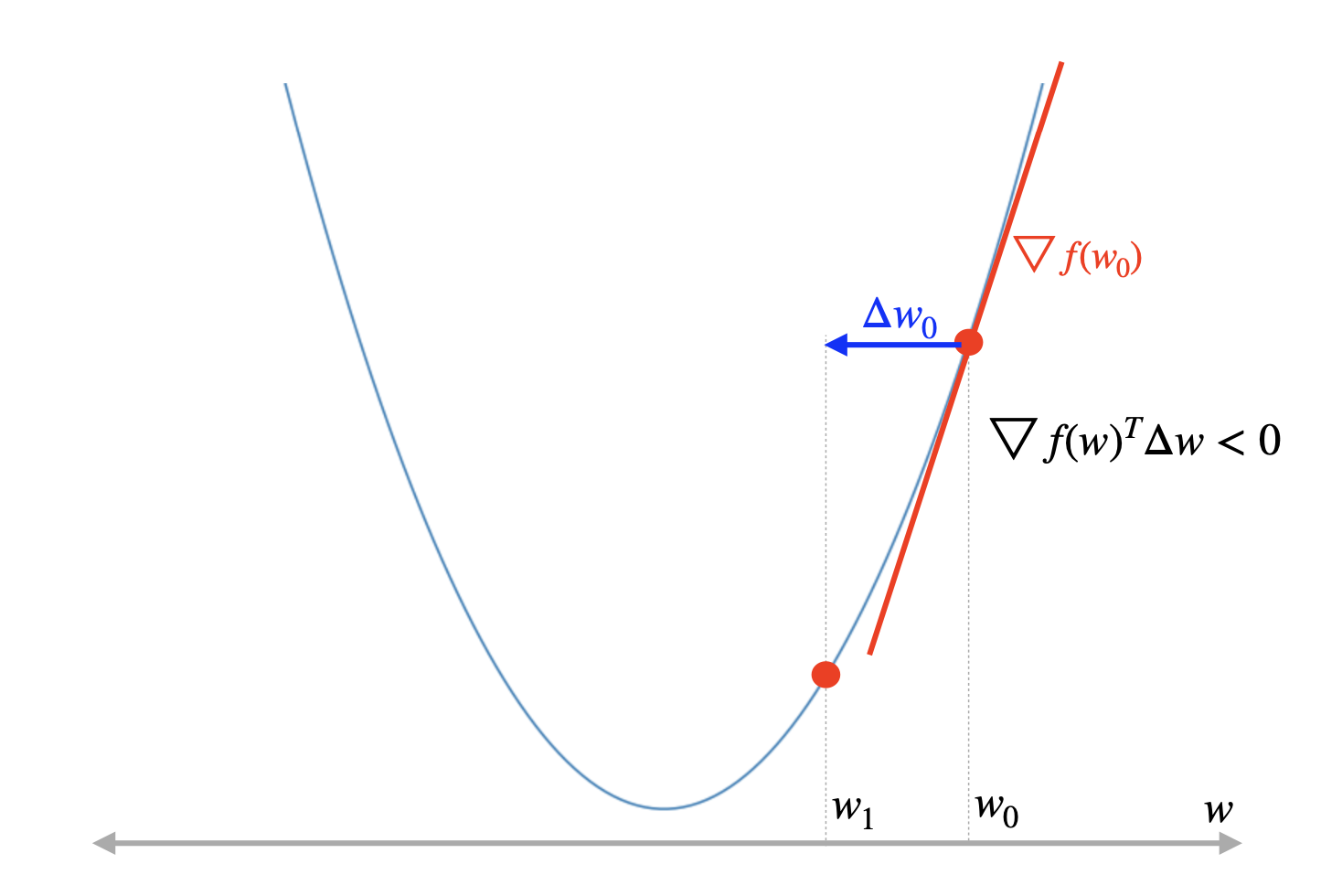
어디로 움직여야 최적의 방향을 찾기 위해 하강하는지 찾는것은 굉장히 쉽다. 접선이 양수 기울기일때는 음수 방향으로 이동하여야하고, 반대로 접선이 음수 기울기일때는 양수 방향으로 이동해주면 된다. (∇𝑓(𝑤)Δw < 0의 부등식을 만족하는 것.)
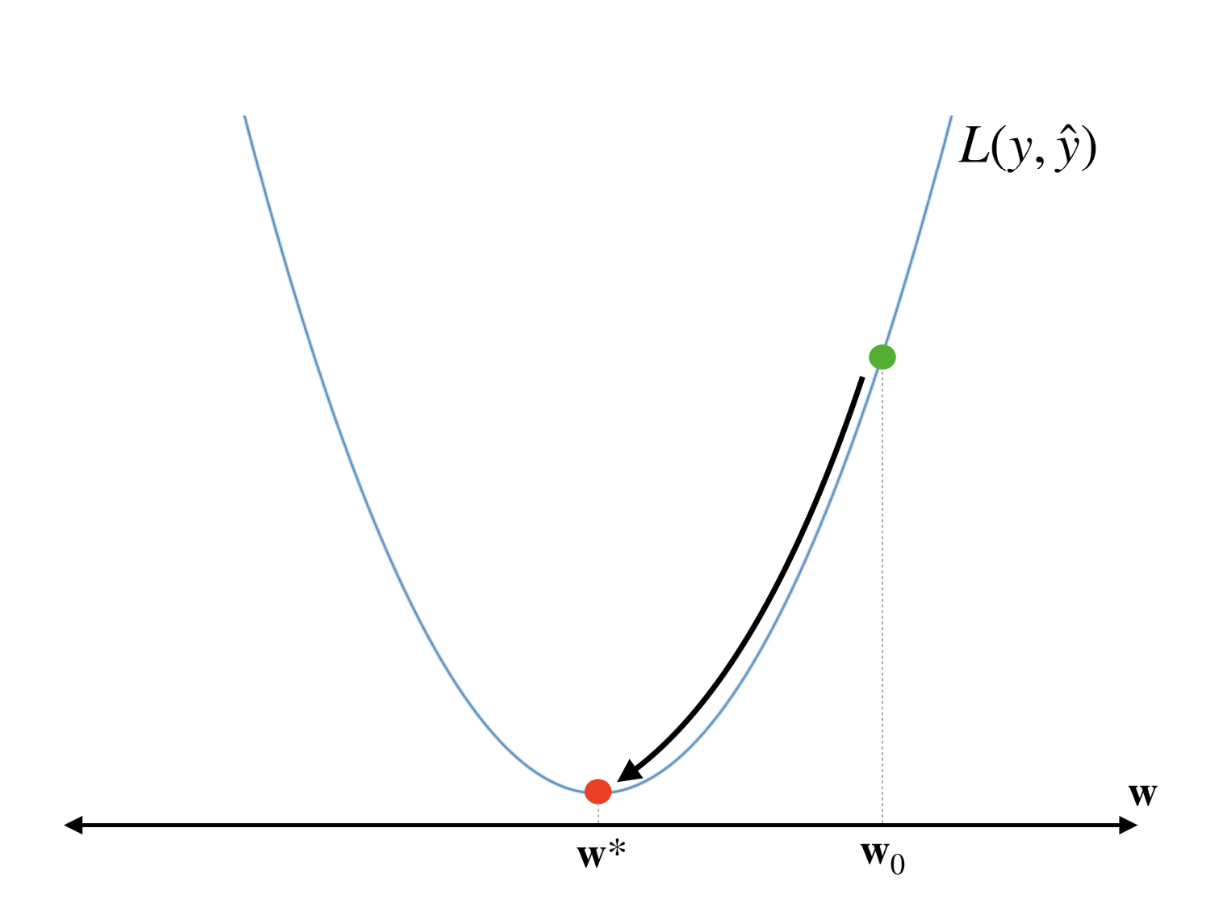
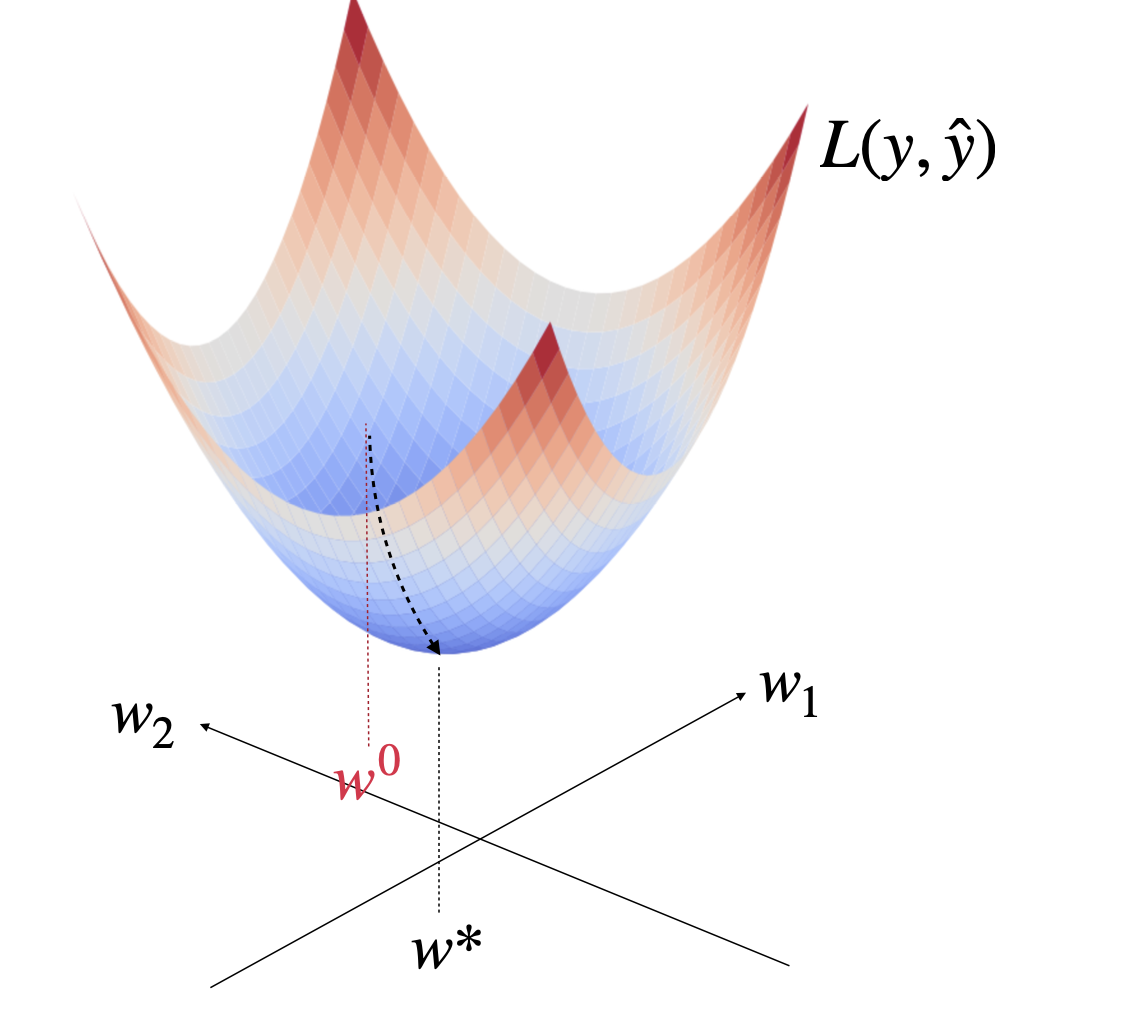
여담으로 하강법에서 중요한 개념 중 하나가 초기값과 로컬 미니멈(Local Minimum)이다.
먼저 초기값은 하강법이 시작하는 지점인 w0의 값이다. 만약 초기값을 잘못 설정하면, 하강법이 전역 최소값(Global Minimum)이 아닌 로컬 미니멈(Local Minimum)에 도달할 수 있다. 로컬 미니멈은 전체 손실 함수에서 가장 작은 값은 아니지만, 주변에서는 더 이상 손실이 줄어들지 않는 지점이다.
이때, 하강법은 기울기가 0이 되는 지점에서 멈추기 때문에, 로컬 미니멈에 빠지면 그곳에서 멈춰버리고 전역 최소값을 찾지 못할 수 있다. 이런 이유로 초기값 설정이 매우 중요하다.
참고 자료
실전 인공지능으로 이어지는 딥러닝 개념 잡기 강의 | 딥러닝호형 - 인프런
딥러닝호형 | 다양한 인공 신경망의 구조와 동작 원리를 이해하고 좋은 모델을 만드는데 필요한 필수 지식을 전달하는 강의입니다., 딥러닝, 기초 개념부터 탄탄하게!인공지능의 핵심 원리를 함
www.inflearn.com
'AI > 개념' 카테고리의 다른 글
| PyTorch 역전파(Backpropagation) 이해하기, 자동 미분과 최적화 (1) | 2025.01.25 |
|---|---|
| PyTorch 텐서(Tensor) 사용법 (0) | 2025.01.25 |
| 손실 함수와 회귀(Regression) (0) | 2024.10.07 |
| 활성화 함수(Activation Function)와 종류 (2) | 2024.10.03 |
| 퍼셉트론 구조와 학습 규칙 (3) | 2024.10.03 |
