개요
본 글에서는 분류 모델의 성능 평가 도구인 혼동행렬에 대해 살펴본다. 혼동행렬의 정의와 구성 요소를 이해하고, 임계값의 필요성과 역할을 분석하며, 혼동행렬이 왜 중요한지, 그리고 이를 활용해 어떠한 성능 평가 지표를 도출할 수 있는지에 대해 설명한다.
혼동행렬의 정의
혼동행렬(confusion matrix)은 분류 모델이 예측한 결과와 실제 정답을 비교하여 모델의 성능을 평가하는 도구이다. 혼동행렬은 보통 다음 네 가지 구성 요소로 이루어진다.
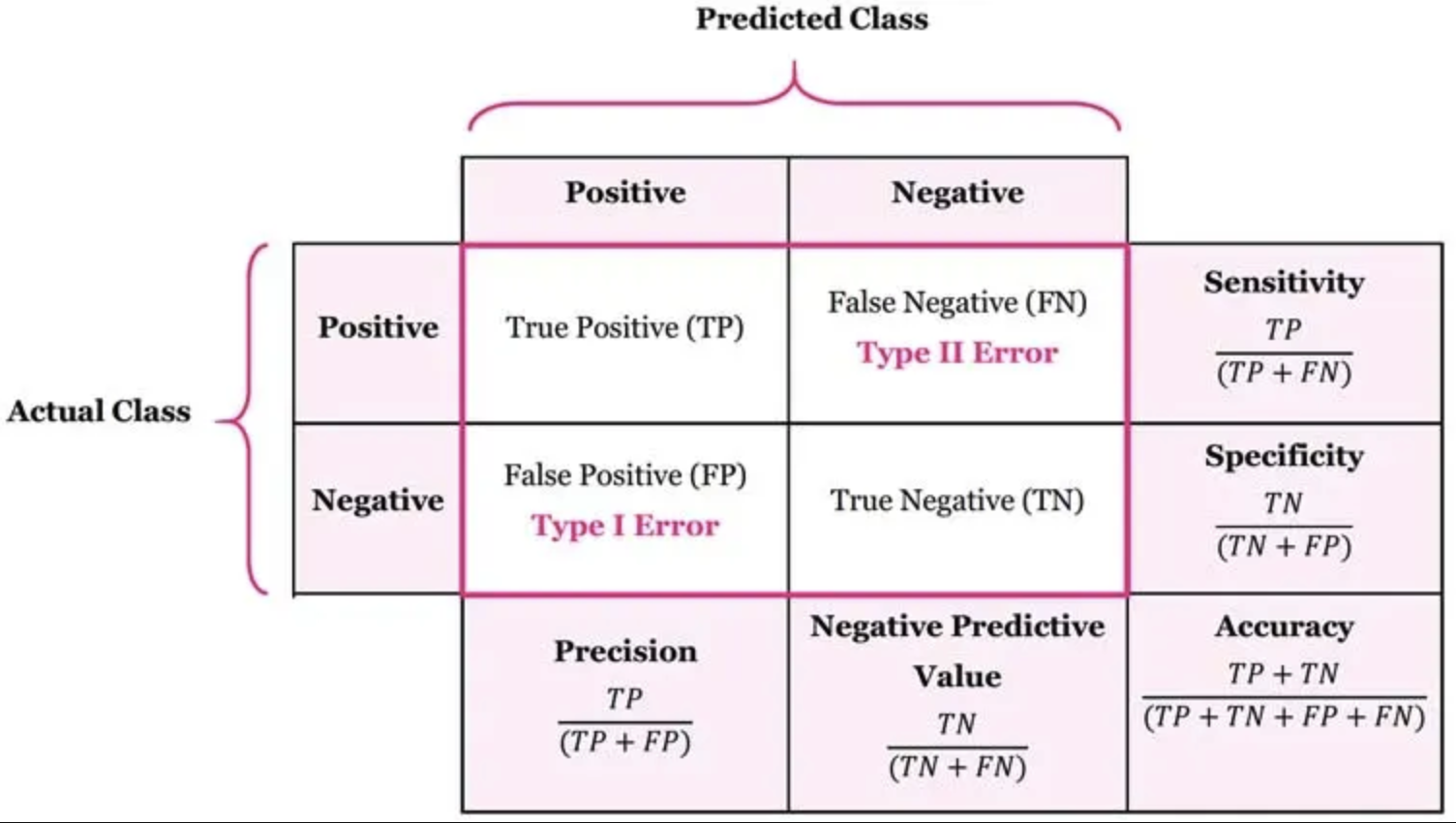
- True Positive (TP): 실제로 긍정인 데이터를 모델이 긍정으로 올바르게 예측한 경우이다.
- False Positive (FP): 실제로 부정인 데이터를 모델이 긍정으로 잘못 예측한 경우이다.
- True Negative (TN): 실제로 부정인 데이터를 모델이 부정으로 올바르게 예측한 경우이다.
- False Negative (FN): 실제로 긍정인 데이터를 모델이 부정으로 잘못 예측한 경우이다.
이 네 가지 요소를 통해 모델이 어떠한 오류를 범하는지, 어느 부분에서 예측이 올바르게 이루어졌는지 세부적으로 분석할 수 있다.
임계값의 필요성과 역할
확률 값을 출력하는 분류 모델에서는 예측 확률을 실제 클래스 레이블로 전환하기 위한 기준인 임계값(threshold)이 필요하다. 임계값은 혼동행렬의 각 요소를 결정하는 데 핵심적인 역할을 한다.
- 예측 결과의 기준 제공:
모델은 입력 데이터에 대해 긍정일 확률을 산출한다. 이 확률을 임계값과 비교하여 예측 결과를 결정한다. 예를 들어, 임계값을 0.5로 설정하면 확률이 0.5 이상일 때 긍정, 미만일 때 부정으로 분류한다. 임계값이 있어야 예측 결과를 명확하게 두 개의 클래스로 나눌 수 있다. - 혼동행렬 구성 요소 결정
임계값의 설정에 따라 TP, FP, TN, FN의 값이 달라진다.- 낮은 임계값을 사용하면 더 많은 데이터가 긍정으로 분류되어 TP와 FP가 증가할 수 있다.
- 높은 임계값을 사용하면 긍정으로 분류되는 데이터가 줄어들어 FP는 감소하지만, 실제 긍정 데이터를 놓쳐 FN이 증가할 수 있다.
이와 같이 임계값은 혼동행렬을 구성하는 데 필수적인 요소이다.
- 모델 성능의 균형 조정
임계값을 조정함으로써 민감도(재현율)와 특이도(정밀도) 사이의 균형을 맞출 수 있다. 임계값의 선택은 모델의 오류 유형에 따라 어느 정도의 오차를 감수할 것인지 결정하는 데 중요한 역할을 한다.
혼동 행렬이 필요한 이유
혼동행렬은 단순한 전체 정확도(Accuracy)만으로는 파악하기 어려운 모델의 세부적인 성능을 분석할 수 있게 한다. 혼동행렬이 필요한 이유는 다음과 같다.
- 세부 성능 분석
전체 정확도는 클래스 불균형 문제로 인해 왜곡될 수 있다. 혼동행렬은 각 클래스별로 올바른 예측과 잘못된 예측을 구분하여, 모델의 약점을 명확하게 드러낸다. - 모델 개선 포인트 도출
False Positive와 False Negative의 비율을 분석함으로써, 모델이 어느 상황에서 오류를 범하는지, 그리고 개선이 필요한 부분이 어디인지를 구체적으로 파악할 수 있다. - 임계값 조정 효과 확인
임계값을 변화시키며 혼동행렬의 각 요소가 어떻게 변하는지 관찰하면, 모델의 민감도와 특이도의 균형을 맞추는 데 필요한 정보를 얻을 수 있다.
참고
혼동행렬
混 同 行 列 / confusion matrix 어떤 개인이나 모델 , 검사도구, 알고리즘 의 진단·분류·판별
namu.wiki
'AI > 개념' 카테고리의 다른 글
| PyTorch 데이터 불러오기 (0) | 2025.02.15 |
|---|---|
| PyTorch 역전파(Backpropagation) 이해하기, 자동 미분과 최적화 (1) | 2025.01.25 |
| PyTorch 텐서(Tensor) 사용법 (0) | 2025.01.25 |
| 최적화 (Optimization)와 목적 함수(Objective Function)과 하강법 (Descent Method) (1) | 2024.10.14 |
| 손실 함수와 회귀(Regression) (0) | 2024.10.07 |
개요
본 글에서는 분류 모델의 성능 평가 도구인 혼동행렬에 대해 살펴본다. 혼동행렬의 정의와 구성 요소를 이해하고, 임계값의 필요성과 역할을 분석하며, 혼동행렬이 왜 중요한지, 그리고 이를 활용해 어떠한 성능 평가 지표를 도출할 수 있는지에 대해 설명한다.
혼동행렬의 정의
혼동행렬(confusion matrix)은 분류 모델이 예측한 결과와 실제 정답을 비교하여 모델의 성능을 평가하는 도구이다. 혼동행렬은 보통 다음 네 가지 구성 요소로 이루어진다.

- True Positive (TP): 실제로 긍정인 데이터를 모델이 긍정으로 올바르게 예측한 경우이다.
- False Positive (FP): 실제로 부정인 데이터를 모델이 긍정으로 잘못 예측한 경우이다.
- True Negative (TN): 실제로 부정인 데이터를 모델이 부정으로 올바르게 예측한 경우이다.
- False Negative (FN): 실제로 긍정인 데이터를 모델이 부정으로 잘못 예측한 경우이다.
이 네 가지 요소를 통해 모델이 어떠한 오류를 범하는지, 어느 부분에서 예측이 올바르게 이루어졌는지 세부적으로 분석할 수 있다.
임계값의 필요성과 역할
확률 값을 출력하는 분류 모델에서는 예측 확률을 실제 클래스 레이블로 전환하기 위한 기준인 임계값(threshold)이 필요하다. 임계값은 혼동행렬의 각 요소를 결정하는 데 핵심적인 역할을 한다.
- 예측 결과의 기준 제공:
모델은 입력 데이터에 대해 긍정일 확률을 산출한다. 이 확률을 임계값과 비교하여 예측 결과를 결정한다. 예를 들어, 임계값을 0.5로 설정하면 확률이 0.5 이상일 때 긍정, 미만일 때 부정으로 분류한다. 임계값이 있어야 예측 결과를 명확하게 두 개의 클래스로 나눌 수 있다. - 혼동행렬 구성 요소 결정
임계값의 설정에 따라 TP, FP, TN, FN의 값이 달라진다.- 낮은 임계값을 사용하면 더 많은 데이터가 긍정으로 분류되어 TP와 FP가 증가할 수 있다.
- 높은 임계값을 사용하면 긍정으로 분류되는 데이터가 줄어들어 FP는 감소하지만, 실제 긍정 데이터를 놓쳐 FN이 증가할 수 있다.
이와 같이 임계값은 혼동행렬을 구성하는 데 필수적인 요소이다.
- 모델 성능의 균형 조정
임계값을 조정함으로써 민감도(재현율)와 특이도(정밀도) 사이의 균형을 맞출 수 있다. 임계값의 선택은 모델의 오류 유형에 따라 어느 정도의 오차를 감수할 것인지 결정하는 데 중요한 역할을 한다.
혼동 행렬이 필요한 이유
혼동행렬은 단순한 전체 정확도(Accuracy)만으로는 파악하기 어려운 모델의 세부적인 성능을 분석할 수 있게 한다. 혼동행렬이 필요한 이유는 다음과 같다.
- 세부 성능 분석
전체 정확도는 클래스 불균형 문제로 인해 왜곡될 수 있다. 혼동행렬은 각 클래스별로 올바른 예측과 잘못된 예측을 구분하여, 모델의 약점을 명확하게 드러낸다. - 모델 개선 포인트 도출
False Positive와 False Negative의 비율을 분석함으로써, 모델이 어느 상황에서 오류를 범하는지, 그리고 개선이 필요한 부분이 어디인지를 구체적으로 파악할 수 있다. - 임계값 조정 효과 확인
임계값을 변화시키며 혼동행렬의 각 요소가 어떻게 변하는지 관찰하면, 모델의 민감도와 특이도의 균형을 맞추는 데 필요한 정보를 얻을 수 있다.
참고
혼동행렬
混 同 行 列 / confusion matrix 어떤 개인이나 모델 , 검사도구, 알고리즘 의 진단·분류·판별
namu.wiki
'AI > 개념' 카테고리의 다른 글
| PyTorch 데이터 불러오기 (0) | 2025.02.15 |
|---|---|
| PyTorch 역전파(Backpropagation) 이해하기, 자동 미분과 최적화 (1) | 2025.01.25 |
| PyTorch 텐서(Tensor) 사용법 (0) | 2025.01.25 |
| 최적화 (Optimization)와 목적 함수(Objective Function)과 하강법 (Descent Method) (1) | 2024.10.14 |
| 손실 함수와 회귀(Regression) (0) | 2024.10.07 |
