MCP 뉴런 (McCulloch-Pitts Neuron)
뉴런을 모방한 인공지능의 시작
인공지능을 설계할 때 인간의 지능이 가장 뛰어나다고 생각한다면, 인간의 뇌를 모방하는 것이 가장 효과적일 것이다. 뉴런의 신호 처리 방식을 이해하면 인공지능의 기초적인 동작 원리를 알 수 있다.
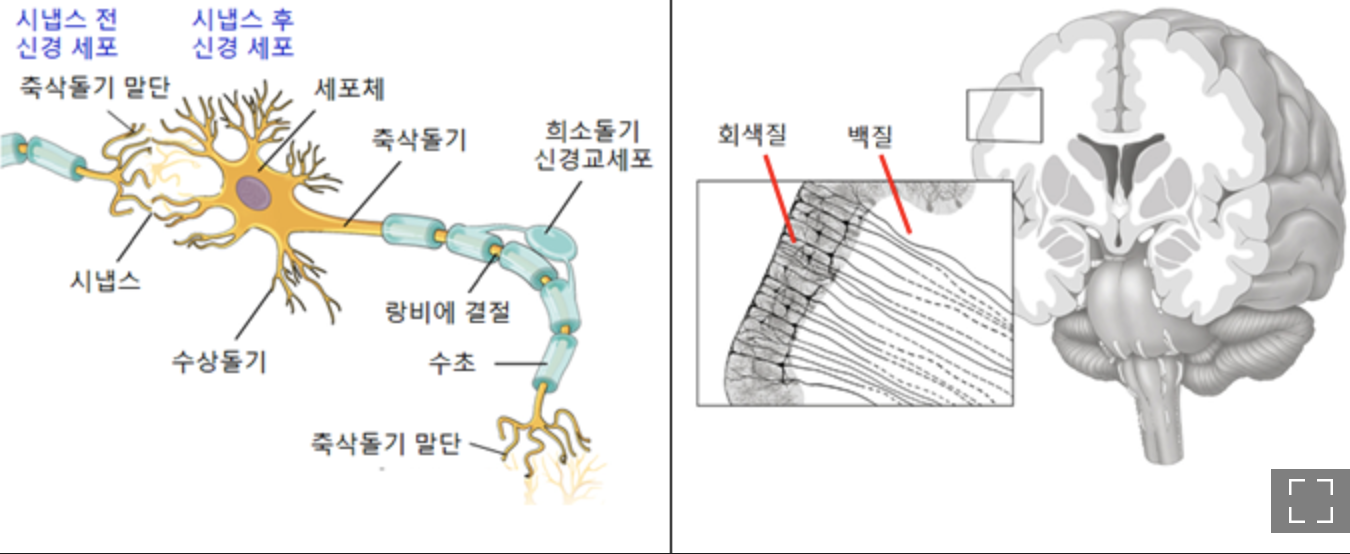
MCP 뉴런이란 무엇인가?
1943년, 신경생리학자인 McCulloch와 수학자인 Pitts가 뉴런의 신경활동을 모방하여 최초의 인공신경망(Artificial Neural Network, ANN)을 제안했다. 이를 MCP 뉴런이라 한다.
MCP 뉴런의 작동 원리
- 입력 신호와 출력 신호
- 입력과 출력 신호는 0 또는 1의 이진 신호다.
- 0은 신호가 없다는 것을 의미하고, 1은 신호가 있다는 것을 의미한다.
- 가중치 (Weight)
- 입력 신호와 곱해지는 값으로, 입력 신호를 활성화(1)하거나 억제(-1)하는 역할을 한다.
- 가중치는 -1 또는 1의 값을 가질 수 있다.
- 합 (Sum)
- 입력 신호와 가중치의 곱을 모두 더한 값이다. 이를 '벡터의 내적'이라고 하며, 수식으로는 Σ(시그마)로 표현한다.
- Σ는 모든 입력 신호와 가중치의 곱을 더하라는 의미다.
- 활성화 함수 (Activation Function)
- 합의 결과를 출력 신호로 변환하는 역할을 한다.
- MCP 뉴런에서 활성화 함수는 임계값(Threshold) 함수를 사용한다.
- 합의 결과가 설정된 임계값보다 크면 출력은 1, 작으면 출력은 0이 된다.
- 수식으로 표현하면, 출력 = 1 if Σ(입력 * 가중치) ≥ 임계값 else 0이다.
프로그래밍으로 구현하기
3개의 데이터 x가 입력되고 임계값이 2인 활성화 함수를 거쳐 1개의 데이터로 출력되는 MCP 뉴런이이 있다
x = [1, 1, 1], w = [1, -1, 1]일 때 출력은?
x = [0, 1, 1], w = [1, -1, 1]일 때 출력은?
파이썬 코드
import numpy as np
x = np.array([1, 1, 1]) # 입력 데이터
w = np.array([1, -1, 1]) # 가중치
Threshold = 2 # 임계값
g = x @ w # 입력 데이터와 가중치 요소간 곱의 합
if g >= Threshold: # 합이 임계값보다 크거나 같으면
y = 1 # 출력은 1
else: # 그렇지 않으면
y = 0 # 출력은 0
print('출력: ', y) # 출력 확인
자바 코드
import java.util.Arrays;
public class McpNeuron {
public static void main(String[] args) {
// 입력 데이터
int[] x = {1, 1, 1};
// 가중치
int[] w = {1, -1, 1};
// 임계값
int threshold = 2;
// 입력 데이터와 가중치 요소간 곱의 합
int g = 0;
for (int i = 0; i < x.length; i++) {
g += x[i] * w[i];
}
// 합이 임계값보다 크거나 같으면 출력은 1, 그렇지 않으면 0
int y = (g >= threshold) ? 1 : 0;
// 출력 확인
System.out.println("출력: " + y);
}
}
MCP 뉴런 (McCulloch-Pitts Neuron) 응용 및 한계점 요약
자동차를 운전하려면 자동차 보유 여부와 운전면허 보유 여부가 모두 충족되어야 운전이 가능하다. 이를 MCP 뉴런으로 표현할 수 있다. 입력 조건에 따라 운전 가능 여부를 출력하는 예제를 통해 확인할 수 있다.

위의 예제에서 가중치 w는 [1, 1]로 설정되고, 임계값 Threshold는 2로 설정된다. 각 조건이 충족될 때만 운전 가능 여부가 1이 된다.
MCP 뉴런의 한계점
MCP 뉴런은 인공신경망의 초기 모델로 의미가 있지만, 여러 한계점이 존재한다.
- 이진 출력값의 한계
- MCP 뉴런은 출력값이 0 또는 1로만 표현되기 때문에, 연속적인 값을 출력해야 하는 문제에는 적합하지 않다. 이로 인해 복잡한 데이터의 예측이나 추론을 제대로 수행할 수 없다.
- 학습 기능 부재
- MCP 뉴런은 입력 데이터와 가중치를 미리 정해진 값으로 사용하므로, 입력에 따른 가중치를 학습하고 조정할 수 있는 기능이 없다. 이는 경험에 기반한 학습을 통해 성능을 개선하는 현대 신경망의 특징과 대비된다.
- 비선형 관계의 모델링 불가
- MCP 뉴런은 복잡한 비선형 관계를 표현할 수 없어, 단순한 결정 경계만 나타낼 수 있다. 이로 인해 실제 생물학적 뉴런의 작동 원리를 구현하기에는 한계가 많으며, 현실적인 문제 해결에 있어서는 제약이 존재한다.
참고 자료
뇌가 발달하면 세상을 경험하는 방식도 변한다 - 매일경제
[송민령의 뇌과학 에세이-11] 선비들이 어렸을 때 쓴 한시를 모은 `한시 이야기`라는 책이 있다. 아이들이 쓴 시조라 재치 있고 귀여운 맛이 있었고, 시조가 지어진 상황에 대한 이야기도 재미있
www.mk.co.kr
'AI > 개념' 카테고리의 다른 글
| PyTorch 텐서(Tensor) 사용법 (0) | 2025.01.25 |
|---|---|
| 최적화 (Optimization)와 목적 함수(Objective Function)과 하강법 (Descent Method) (1) | 2024.10.14 |
| 손실 함수와 회귀(Regression) (0) | 2024.10.07 |
| 활성화 함수(Activation Function)와 종류 (2) | 2024.10.03 |
| 퍼셉트론 구조와 학습 규칙 (3) | 2024.10.03 |
MCP 뉴런 (McCulloch-Pitts Neuron)
뉴런을 모방한 인공지능의 시작
인공지능을 설계할 때 인간의 지능이 가장 뛰어나다고 생각한다면, 인간의 뇌를 모방하는 것이 가장 효과적일 것이다. 뉴런의 신호 처리 방식을 이해하면 인공지능의 기초적인 동작 원리를 알 수 있다.

MCP 뉴런이란 무엇인가?
1943년, 신경생리학자인 McCulloch와 수학자인 Pitts가 뉴런의 신경활동을 모방하여 최초의 인공신경망(Artificial Neural Network, ANN)을 제안했다. 이를 MCP 뉴런이라 한다.
MCP 뉴런의 작동 원리
- 입력 신호와 출력 신호
- 입력과 출력 신호는 0 또는 1의 이진 신호다.
- 0은 신호가 없다는 것을 의미하고, 1은 신호가 있다는 것을 의미한다.
- 가중치 (Weight)
- 입력 신호와 곱해지는 값으로, 입력 신호를 활성화(1)하거나 억제(-1)하는 역할을 한다.
- 가중치는 -1 또는 1의 값을 가질 수 있다.
- 합 (Sum)
- 입력 신호와 가중치의 곱을 모두 더한 값이다. 이를 '벡터의 내적'이라고 하며, 수식으로는 Σ(시그마)로 표현한다.
- Σ는 모든 입력 신호와 가중치의 곱을 더하라는 의미다.
- 활성화 함수 (Activation Function)
- 합의 결과를 출력 신호로 변환하는 역할을 한다.
- MCP 뉴런에서 활성화 함수는 임계값(Threshold) 함수를 사용한다.
- 합의 결과가 설정된 임계값보다 크면 출력은 1, 작으면 출력은 0이 된다.
- 수식으로 표현하면, 출력 = 1 if Σ(입력 * 가중치) ≥ 임계값 else 0이다.
프로그래밍으로 구현하기
3개의 데이터 x가 입력되고 임계값이 2인 활성화 함수를 거쳐 1개의 데이터로 출력되는 MCP 뉴런이이 있다
x = [1, 1, 1], w = [1, -1, 1]일 때 출력은?
x = [0, 1, 1], w = [1, -1, 1]일 때 출력은?
파이썬 코드
import numpy as np
x = np.array([1, 1, 1]) # 입력 데이터
w = np.array([1, -1, 1]) # 가중치
Threshold = 2 # 임계값
g = x @ w # 입력 데이터와 가중치 요소간 곱의 합
if g >= Threshold: # 합이 임계값보다 크거나 같으면
y = 1 # 출력은 1
else: # 그렇지 않으면
y = 0 # 출력은 0
print('출력: ', y) # 출력 확인
자바 코드
import java.util.Arrays;
public class McpNeuron {
public static void main(String[] args) {
// 입력 데이터
int[] x = {1, 1, 1};
// 가중치
int[] w = {1, -1, 1};
// 임계값
int threshold = 2;
// 입력 데이터와 가중치 요소간 곱의 합
int g = 0;
for (int i = 0; i < x.length; i++) {
g += x[i] * w[i];
}
// 합이 임계값보다 크거나 같으면 출력은 1, 그렇지 않으면 0
int y = (g >= threshold) ? 1 : 0;
// 출력 확인
System.out.println("출력: " + y);
}
}
MCP 뉴런 (McCulloch-Pitts Neuron) 응용 및 한계점 요약
자동차를 운전하려면 자동차 보유 여부와 운전면허 보유 여부가 모두 충족되어야 운전이 가능하다. 이를 MCP 뉴런으로 표현할 수 있다. 입력 조건에 따라 운전 가능 여부를 출력하는 예제를 통해 확인할 수 있다.

위의 예제에서 가중치 w는 [1, 1]로 설정되고, 임계값 Threshold는 2로 설정된다. 각 조건이 충족될 때만 운전 가능 여부가 1이 된다.
MCP 뉴런의 한계점
MCP 뉴런은 인공신경망의 초기 모델로 의미가 있지만, 여러 한계점이 존재한다.
- 이진 출력값의 한계
- MCP 뉴런은 출력값이 0 또는 1로만 표현되기 때문에, 연속적인 값을 출력해야 하는 문제에는 적합하지 않다. 이로 인해 복잡한 데이터의 예측이나 추론을 제대로 수행할 수 없다.
- 학습 기능 부재
- MCP 뉴런은 입력 데이터와 가중치를 미리 정해진 값으로 사용하므로, 입력에 따른 가중치를 학습하고 조정할 수 있는 기능이 없다. 이는 경험에 기반한 학습을 통해 성능을 개선하는 현대 신경망의 특징과 대비된다.
- 비선형 관계의 모델링 불가
- MCP 뉴런은 복잡한 비선형 관계를 표현할 수 없어, 단순한 결정 경계만 나타낼 수 있다. 이로 인해 실제 생물학적 뉴런의 작동 원리를 구현하기에는 한계가 많으며, 현실적인 문제 해결에 있어서는 제약이 존재한다.
참고 자료
뇌가 발달하면 세상을 경험하는 방식도 변한다 - 매일경제
[송민령의 뇌과학 에세이-11] 선비들이 어렸을 때 쓴 한시를 모은 `한시 이야기`라는 책이 있다. 아이들이 쓴 시조라 재치 있고 귀여운 맛이 있었고, 시조가 지어진 상황에 대한 이야기도 재미있
www.mk.co.kr
'AI > 개념' 카테고리의 다른 글
| PyTorch 텐서(Tensor) 사용법 (0) | 2025.01.25 |
|---|---|
| 최적화 (Optimization)와 목적 함수(Objective Function)과 하강법 (Descent Method) (1) | 2024.10.14 |
| 손실 함수와 회귀(Regression) (0) | 2024.10.07 |
| 활성화 함수(Activation Function)와 종류 (2) | 2024.10.03 |
| 퍼셉트론 구조와 학습 규칙 (3) | 2024.10.03 |
