퍼셉트론 구조와 학습 규칙
퍼셉트론의 등장 배경
퍼셉트론은 ‘percept(인지하다)’와 ‘neuron(뉴런)’의 합성어로, 인간의 뇌가 정보를 처리하는 방식을 모방한 인공 신경망이다. MCP 뉴런이 가진 여러 한계점을 극복하기 위해 만들어졌으며, 특히 데이터를 학습하고 조정하는 능력을 갖추고 있다.
MCP 뉴런의 한계점과 퍼셉트론의 특징
- 학습 규칙의 부재
- MCP 뉴런은 입력에 대한 가중치와 임계값을 미리 사람이 정해야 한다. 이렇게 고정된 구조는 새로운 데이터에 유연하게 대처하지 못하는 문제를 발생시킨다.
- 해결 방안: 퍼셉트론은 학습 알고리즘을 통해 가중치를 스스로 조정한다. 즉, 학습된 데이터를 바탕으로 새로운 데이터에 대해서도 예측이 가능해지도록 설계되었다. 이를 통해 예측 성능을 지속적으로 향상시킬 수 있다.
- MCP 뉴런은 입력에 대한 가중치와 임계값을 미리 사람이 정해야 한다. 이렇게 고정된 구조는 새로운 데이터에 유연하게 대처하지 못하는 문제를 발생시킨다.
- 이진 가중치의 한계
- MCP 뉴런은 가중치 값이 -1과 1의 이진 값만 가지기 때문에, 입력이 활성화되거나 억제되는 단순한 결과만 나타낼 수 있다. 이 방식은 연속적인 입력 값을 세밀하게 표현하지 못하는 한계가 있다.
- 해결 방안: 퍼셉트론은 연속적인 가중치를 허용함으로써, 다양한 입력 값에 대해 더 정확한 예측을 가능하게 한다.
- MCP 뉴런은 가중치 값이 -1과 1의 이진 값만 가지기 때문에, 입력이 활성화되거나 억제되는 단순한 결과만 나타낼 수 있다. 이 방식은 연속적인 입력 값을 세밀하게 표현하지 못하는 한계가 있다.
- 편향(bias) 값의 도입
- MCP 뉴런은 입력 신호와 가중치의 곱을 단순히 합한 값을 기준으로 임계값을 초과할 때만 활성화 여부를 결정한다. 그러나 편향이 없으면 특정 입력 패턴에서 항상 같은 결과가 나타날 수 있다.
- 해결 방안: 퍼셉트론은 편향(bias)을 도입하여 예측 결과를 조정하고, 입력 신호가 특정 기준에 따라 유연하게 반응할 수 있도록 한다. 편향은 입력 신호가 없는 경우에도 모델이 활성화될 수 있도록 도움을 준다.
- MCP 뉴런은 입력 신호와 가중치의 곱을 단순히 합한 값을 기준으로 임계값을 초과할 때만 활성화 여부를 결정한다. 그러나 편향이 없으면 특정 입력 패턴에서 항상 같은 결과가 나타날 수 있다.
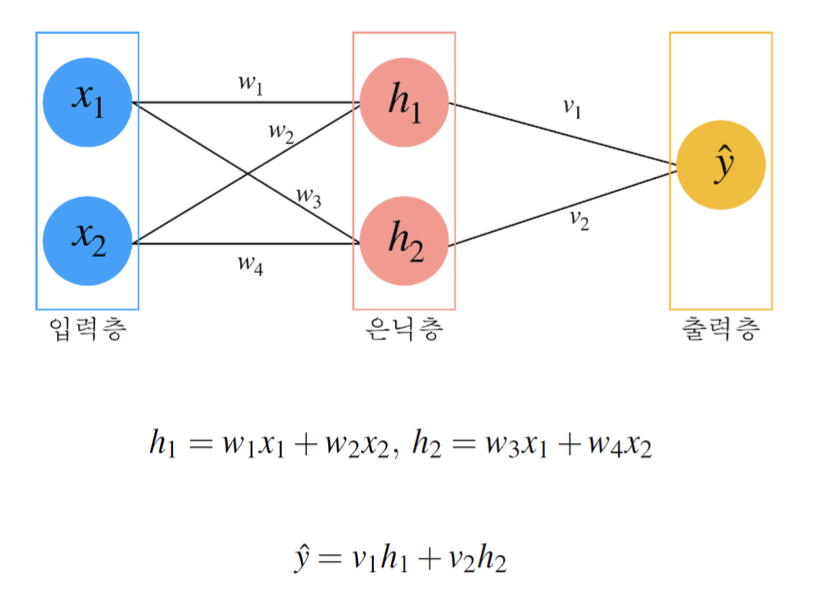
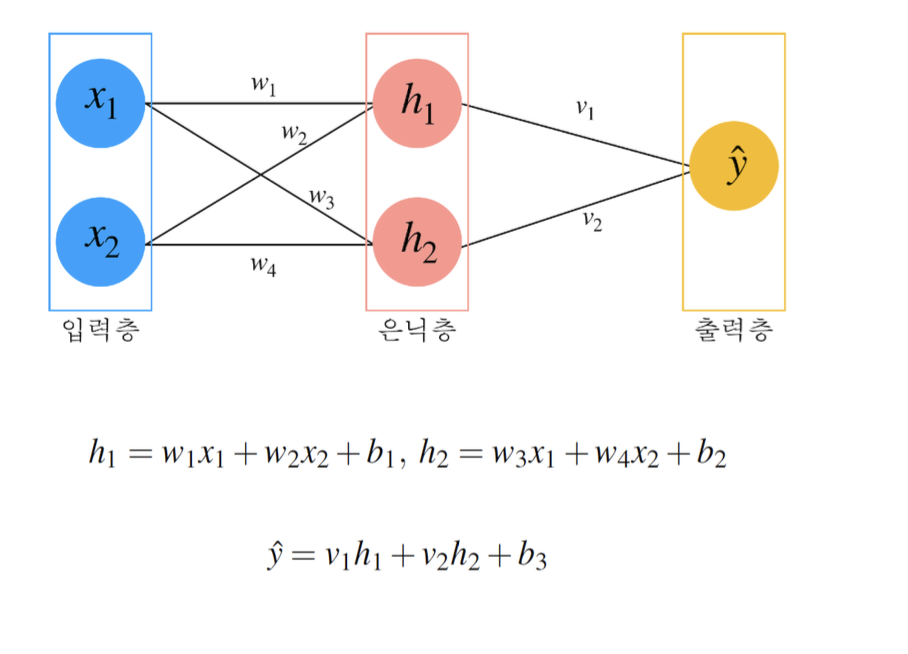

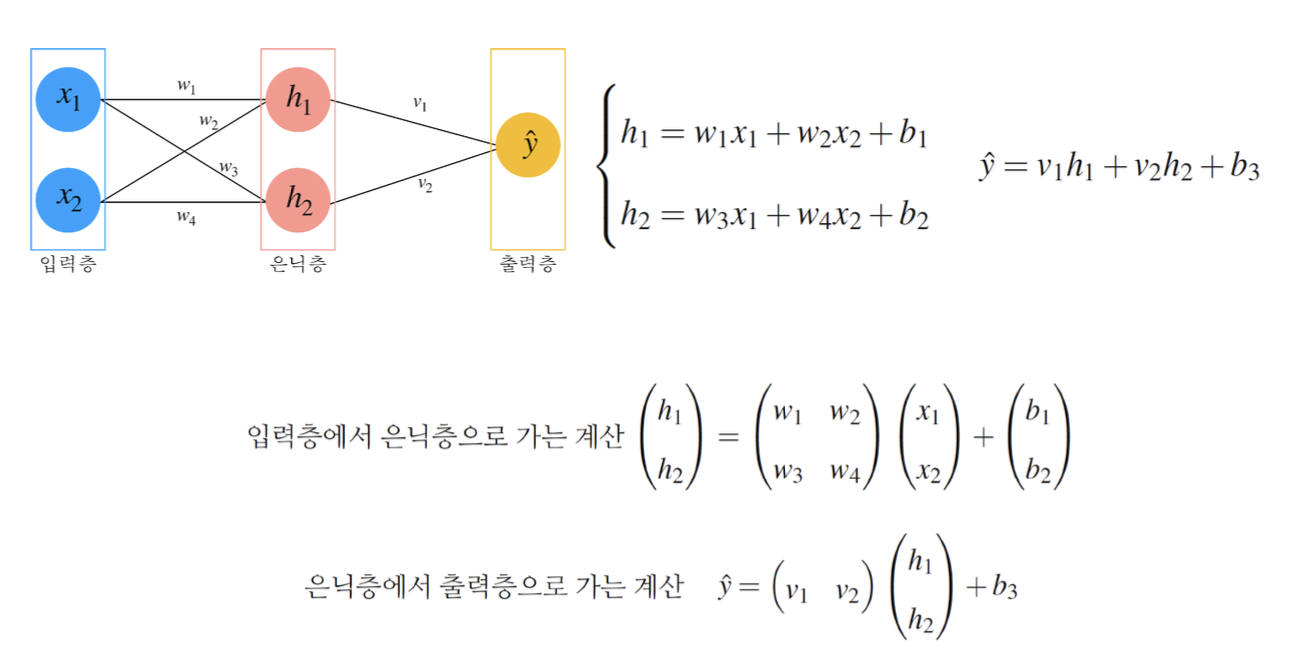
퍼셉트론의 구조
퍼셉트론은 입력층, 집계 함수, 임계 함수, 출력 값으로 구성된다. 각 구성 요소는 다음과 같다.
- 입력 단위 (Input Units)
- 입력 데이터의 각 특성을 요소로 가지며, 모델에 들어오는 모든 정보는 이 입력 단위에 포함된다. 예를 들어, x라는 데이터가 있을 때, x는 [x1, x2, x3]과 같은 여러 특성 값을 포함할 수 있다.
- 집계 함수 (Aggregation Function)
- 입력 데이터와 가중치를 곱한 뒤, 모든 값을 더한 결과를 생성한다. 기존 MCP 뉴런에서는 단순한 가중치와 입력 값의 곱의 합이었다면, 퍼셉트론에서는 편향 값이 더해져 Σ(x*w) + bias의 형태로 확장된다.
- 임계 함수 (Threshold Function)
- 집계 함수의 결과가 특정 임계값을 초과할 때 활성화 상태로 설정한다. 이는 퍼셉트론의 예측 결과를 출력하기 위한 최소한의 자극을 결정하는 역할을 한다.
- 출력 값 (Output)
- 임계 함수의 결과로 출력 값이 생성된다. 퍼셉트론의 기본 구조에서는 출력 값이 -1 또는 1의 값을 가지며, 이는 이진 분류 문제에서 사용될 수 있다.

퍼셉트론의 학습 규칙
퍼셉트론은 학습 규칙을 통해 예측의 오차를 줄여 나가며 가중치와 편향을 조정한다. 학습 과정은 크게 오차(error) 계산과 가중치 조정(weight update)으로 이루어진다.
- 오차 (Error)
- 오차는 모델이 예측한 값과 실제 값의 차이로, 모델이 얼마나 부정확한지 나타낸다. 오차가 크면 모델이 잘못 예측한 것이므로, 이를 줄이기 위해 가중치와 편향 값을 조정해야 한다.
- 오차 계산 (Error Computation)
- 오차를 계산하고, 그에 따라 가중치를 얼마나 변화시킬지 결정한다. 이때 중요한 요소는 학습률(learning rate, η), 오차(error), 그리고 입력 요소 값이다.
- 공식은 다음과 같다
- Δw_i = η × error × x_i
- Δw_i: i번째 가중치의 변화량을 의미한다.
- η (learning rate): 학습률로, 가중치를 얼마나 변화시킬지 결정하는 상수이다. 0과 1 사이의 값을 가지며, 값이 클수록 변화 폭이 커진다.
- error: 예측값과 실제값의 차이를 의미한다. 오차가 크면 가중치 변화량도 더 커진다.
- x_i: i번째 입력 요소로, 입력 값이 클수록 가중치 변화량에 더 큰 영향을 미친다.
- Δw_i = η × error × x_i
- 가중치 업데이트 (Weight Update)
- 학습 규칙에 따라 계산된 가중치 변화량을 기존 가중치에 더해준다. 이 과정을 반복하면서 가중치는 점차 최적화된다.
- 가중치 업데이트 공식은 다음과 같다
- wi_(new)=w_i(old)+Δw_i
- 여러 번의 반복 학습을 통해 오차가 0에 가까워지면, 더 이상 학습을 진행하지 않고 학습을 종료한다.
퍼셉트론 학습의 예시
퍼셉트론 학습 과정을 이해하기 위해 간단한 예제를 살펴보자.
- 입력값과 목표값 설정: 예를 들어, 입력값 x = [1, -1, 0.5]와 목표 출력 y = 1이 있다고 하자.
- 가중치 초기화: 초기 가중치를 w = [0.5, -0.5, 0.5]로 설정한다.
- 오차 계산: 예측된 출력과 목표값의 차이를 계산하여 오차를 구한다.
- 가중치 변화량 계산: 학습률(η), 오차(error), 입력값(x)을 곱하여 가중치 변화량을 계산한다.
- 가중치 업데이트: 기존 가중치에 변화량을 더하여 새로운 가중치를 얻는다.
- 반복 학습: 오차가 0에 가까워질 때까지 위 과정을 반복한다.
퍼셉트론 구현 및 학습 요약
파이썬으로 퍼셉트론 구현
먼저, 퍼셉트론을 구현하기 위해 필요한 변수들을 정의하고 초기화한다.
import numpy as np
np.random.seed(42) # 랜덤 시드 설정으로 동일한 결과를 재현
X = np.array([0.5, 0.5, 0.5]) # 입력 데이터
W = np.random.rand(3) # 가중치 초기화 (0과 1 사이의 임의 값 3개)
B = np.random.rand(1) # 편향 초기화 (0과 1 사이의 임의 값 1개)
Y = np.array([-1]) # 목표 출력값 (1개 요소를 갖는 Numpy 배열)
print('W: ', W) # 가중치 출력
print('B: ', B) # 편향 출력
출력 결과
W: [0.37454012 0.95071431 0.73199394]
B: [0.59865848]
- 입력 데이터 (X): 값이 각각 0.5인 3개의 요소로 이루어진 배열.
- 가중치 (W): 0과 1 사이의 임의 값 3개로 초기화된 배열.
- 편향 (B): 0과 1 사이의 임의 값 1개로 초기화된 배열.
- 목표 출력값 (Y): 예측해야 하는 정답 값으로, 여기서는 -1로 설정.
이후 입력 데이터와 가중치를 사용하여 예측값을 계산하는 함수를 정의한다.
def predict_func(x, w, b):
# 집계 함수: 가중치와 입력값의 곱의 합에 편향을 더한 값
z = x @ w + b
# 임계값 함수: z가 0보다 크면 1, 그렇지 않으면 -1
if z > 0:
predict = 1
else:
predict = -1
return predict
predict = predict_func(X, W, B)
print(predict)
출력 결과
1
퍼셉트론 학습 규칙을 사용하여 가중치와 편향을 조정하는 학습 과정을 구현한다.
learning_rate = 0.1 # 학습률 설정
num_epochs = 10 # 에폭 횟수 설정
for epoch in range(num_epochs):
y_hat = predict_func(X, W, B) # 예측값 계산
error = Y - y_hat # 오차 계산
W = W + learning_rate * X * error # 가중치 업데이트
B = B + learning_rate * error # 편향 업데이트
print('Epoch: ', epoch, 'Error : ', error[0]) # 에폭과 오차 출력
출력 결과
Epoch: 0 Error : -2
Epoch: 1 Error : -2
Epoch: 2 Error : -2
Epoch: 3 Error : -2
Epoch: 4 Error : -2
Epoch: 5 Error : 0
Epoch: 6 Error : 0
Epoch: 7 Error : 0
Epoch: 8 Error : 0
Epoch: 9 Error : 0
- 순전파(Forward Pass): 입력값과 가중치를 곱하고 편향을 더해 예측값을 도출.
- 오차 계산: 목표값(Y)과 예측값(y_hat)의 차이를 계산하여 오차를 구함.
- 가중치 및 편향 업데이트: 학습률, 입력값, 오차를 사용하여 가중치와 편향을 수정.
- 출력 확인: 각 에폭마다 오차를 출력하여 학습 진행 상황을 확인.
학습이 완료된 후 가중치, 편향, 예측값을 확인하고 학습의 성공 여부를 평가한다.
print('Trained Weights: ', W) # 학습된 가중치 확인
print('Trained Bias: ', B) # 학습된 편향 확인
predict = predict_func(X, W, B) # 예측값 계산
print('predict: ', predict) # 예측값 출력
z = X @ W + B # 집계값 계산
print('z: ', z) # 집계값 출력
출력 결과
Trained Weights: [0.17454012 0.75071431 0.53199394]
Trained Bias: [0.19865848]
predict: -1
z: [-0.12271733]
자바로 퍼셉트론 구현
import java.util.Random;
public class Perceptron {
public static void main(String[] args) {
// 난수 생성을 위한 Random 객체 생성 및 시드값 설정
Random rand = new Random(42);
// 입력 데이터 정의
double[] X = {0.5, 0.5, 0.5};
// 가중치 초기화 (랜덤 값 생성)
double[] W = new double[3];
for (int i = 0; i < W.length; i++) {
W[i] = rand.nextDouble(); // 0과 1 사이의 랜덤 값
}
// 편향 초기화
double B = rand.nextDouble();
// 목표 출력값 정의
double Y = -1;
// 가중치와 편향 출력
System.out.print("W: ");
for (double w : W) {
System.out.print(w + " ");
}
System.out.println();
System.out.println("B: " + B);
// 예측 함수 호출 및 결과 출력
double predict = predictFunc(X, W, B);
System.out.println("Initial Prediction: " + predict);
// 학습 실행
trainPerceptron(X, W, B, Y, 0.1, 10);
}
// 예측 함수 정의
public static double predictFunc(double[] x, double[] w, double b) {
double z = 0;
// 집계함수: 입력 데이터와 가중치의 곱을 모두 더하고, 편향을 더함
for (int i = 0; i < x.length; i++) {
z += x[i] * w[i];
}
z += b;
// 임계 함수: z 값이 0보다 크면 1, 작으면 -1 반환
return z > 0 ? 1 : -1;
}
// 퍼셉트론 학습 함수 정의
public static void trainPerceptron(double[] X, double[] W, double B, double Y, double learningRate, int numEpochs) {
for (int epoch = 0; epoch < numEpochs; epoch++) {
// 예측값 계산
double y_hat = predictFunc(X, W, B);
// 오차 계산
double error = Y - y_hat;
// 가중치 업데이트
for (int i = 0; i < W.length; i++) {
W[i] = W[i] + learningRate * X[i] * error;
}
// 편향 업데이트
B = B + learningRate * error;
// 에폭과 오차 출력
System.out.println("Epoch: " + epoch + " Error: " + error);
// 오차가 0이면 학습 종료
if (error == 0) {
break;
}
}
// 학습이 끝난 후 가중치와 편향 출력
System.out.print("Trained Weights: ");
for (double w : W) {
System.out.print(w + " ");
}
System.out.println();
System.out.println("Trained Bias: " + B);
// 학습 후 예측 값 확인
double finalPrediction = predictFunc(X, W, B);
System.out.println("Final Prediction: " + finalPrediction);
}
}
참고 자료
03-1 퍼셉트론 구조
## 1. MCP을 넘어서 퍼셉트론은 percept(무언가를 인지하는 능력) + neuron(뉴런)의 합성어로 생물학적 뉴런이 감각 정보를 받아 문제를 해결하는 원리를 따라한 …
wikidocs.net
2-1 퍼셉트론의 구성 및 동작 원리
#### 2-1-1 퍼셉트론이란? 퍼셉트론은 매컬룩/피츠의 연구를 기반으로 로젠블렛이 개발한 인공지능 알고리즘이다. 앞서 1장에서 말했듯이 처음 로젠블렛은 IBM 704 컴퓨…
wikidocs.net
실전 인공지능으로 이어지는 딥러닝 개념 잡기 강의 | 딥러닝호형 - 인프런
딥러닝호형 | 다양한 인공 신경망의 구조와 동작 원리를 이해하고 좋은 모델을 만드는데 필요한 필수 지식을 전달하는 강의입니다., 딥러닝, 기초 개념부터 탄탄하게!인공지능의 핵심 원리를 함
www.inflearn.com
'AI > 개념' 카테고리의 다른 글
| PyTorch 텐서(Tensor) 사용법 (0) | 2025.01.25 |
|---|---|
| 최적화 (Optimization)와 목적 함수(Objective Function)과 하강법 (Descent Method) (1) | 2024.10.14 |
| 손실 함수와 회귀(Regression) (0) | 2024.10.07 |
| 활성화 함수(Activation Function)와 종류 (2) | 2024.10.03 |
| MCP 뉴런 (0) | 2024.10.02 |
